Combinatorics

Introduction to Combinatorics:

What is combinatorics: Combinatorics is a branch of mathematics primarily concerned with counting and certain properties of finite structures.

It deals with the study of enumeration, combination, and permutation of sets of elements and the mathematical relations that characterize their properties.

In other word we can also that Combinatorics is all about number of ways of choosing some objects out of a collection and/or number of ways of their arrangement. For example suppose there are five members in a club, let’s say there names are A, B, C, D, and E, and one of them is to be chosen as the coordinator. Clearly any one out of them can be chosen so there are 5 ways. Now suppose two members are to be chosen for the position of coordinator and co-coordinator. Now, we can choose A as coordinator and one out of the rest 4 as co-coordinator. Similarly we can choose B as coordinator and one of out the remaining 4 as co-coordinator, and similarly with C, D and E. So there will be total 20 possible ways.

Basic Combinatorics Rules:

Suppose there are two sets A and B.

The basic rules of combinatorics one must remember are:

The Rule of Product:
The product rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X×Y number of ways to choose two elements, one from A and one from B.
The Rule of Sum:
The sum rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X+Y number of ways to choose one element that can belong to either A or to B.
Rule of Inclusion-Exclusion :

The principle of inclusion-exclusion says that in order to count only unique ways of doing a task, we must add the number of ways to do it in one way and the number of ways to do it in another and then subtract the number of ways to do the task that are common to both sets of ways. The principle of inclusion-exclusion is also known as the subtraction principle.

For any set A and B,

|A U B| = |A| + |B| - |A $\cap$ B|.

These rules can be used for a finite collection of sets.

Examples:

Example 1 – In how many ways can 3 winning prizes be given to the top 3 players in a game played by 12 players?

Solution – We have to distribute 3 prizes among 12 players. This task can be divided into 3 subtasks of assigning a single prize to a certain player.

Giving out the first prize can be done in 12 different ways. After giving out the first prize, two prizes remain and 11 players remain. Similarly, the second prize and third prize can be given in 11 ways and 10 ways. The total number of ways by the product rule is 12 * 11 * 10 = 1320.

Example 2 – How many distinct license plates are possible in the given format- Two alphabets in uppercase, followed by two digits then a hyphen, and finally four digits. Sample- AB12-3456.

Solution – There are 26 possibilities for each of the two letters and 10 possibilities for each of the digits. Therefore, the total number of possibilities is – 26 * 26 * 10 * 10 * 10 * 10 * 10 * 10 = 676000000.

Example 3 – How many variable names of length up to 3 exist if the variable names are alphanumeric and case-sensitive with the restriction that the first character has to be an alphabet?

Solution – Let N1, N2, and N3 denote the number of possible variable names of lengths 1, 2, and 3. Therefore, the total number of variable names is N1 + N2 + N3.

For N1, there are only 52 possibilities since the first character has to be an alphabet.

For N2, there are 52 * 62 = 3224 possibilities.

For N3, there are 52 * 62 * 62 = 199888 possibilities.

Therefore, total number of variable names = 52 + 3224 + 199888 = 203164

Example 4 – How many binary strings of length 8 either start with a ‘1’ bit or end with two bits ’00’?

Solution – If the string starts with one, there are 7 characters left which can be filled in 2^7 = 128 ways. If the string ends with ’00’ then 6 characters can be filled in 2^6 = 64 ways. Now if we add the above sets of ways and conclude that it is the final answer, then it would be wrong. This is because there are strings with start with ‘1’ and end with ’00’ both, and since they satisfy both criteria they are counted twice. So we need to subtract such strings to get a correct count. Strings that start with ‘1’ and end with ’00’ have five characters that can be filled in 2^5 = 32 ways.

So by the inclusion-exclusion principle we get –

Total strings = 128 + 64 – 32 = 160.

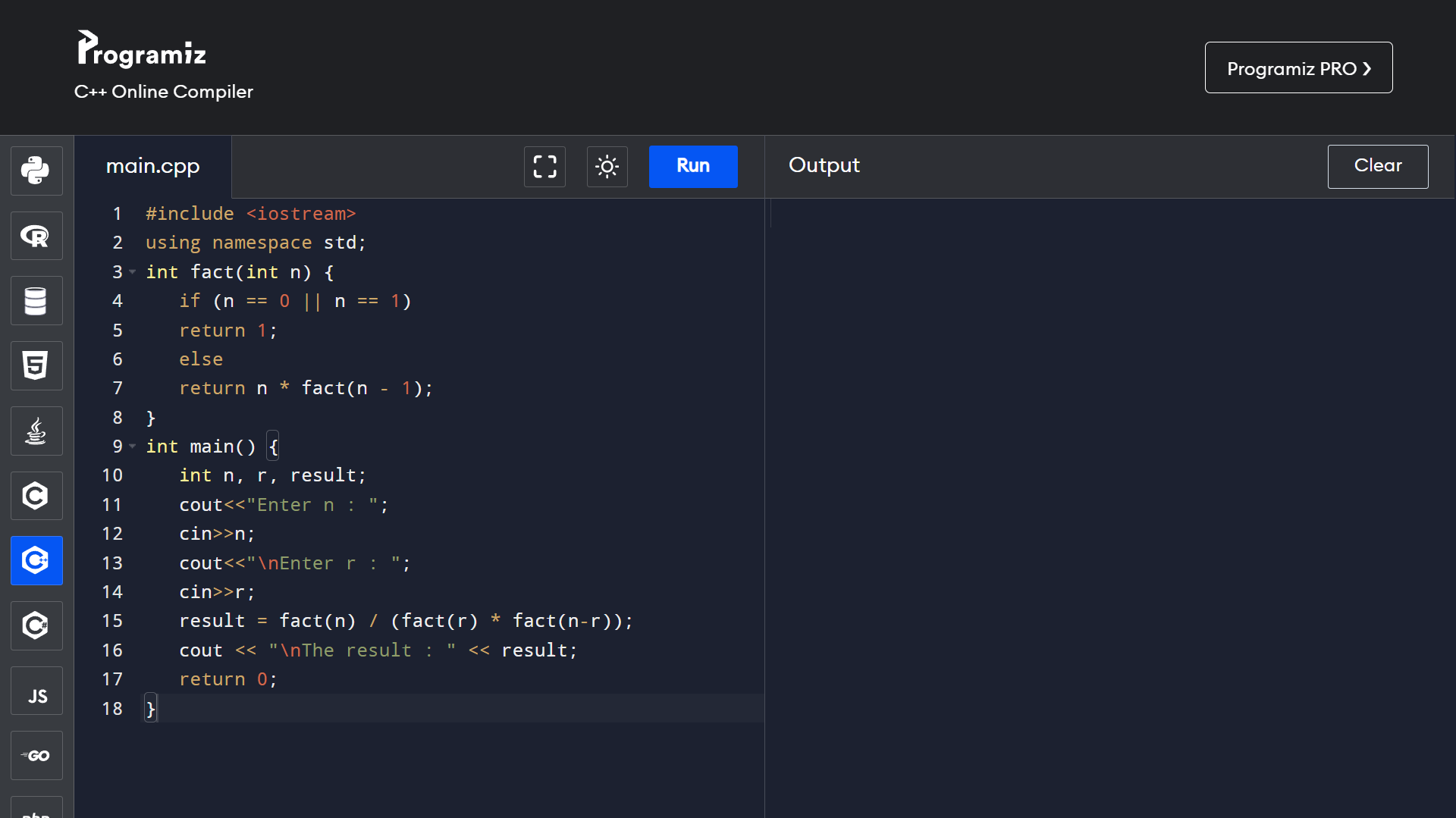
Factorials:

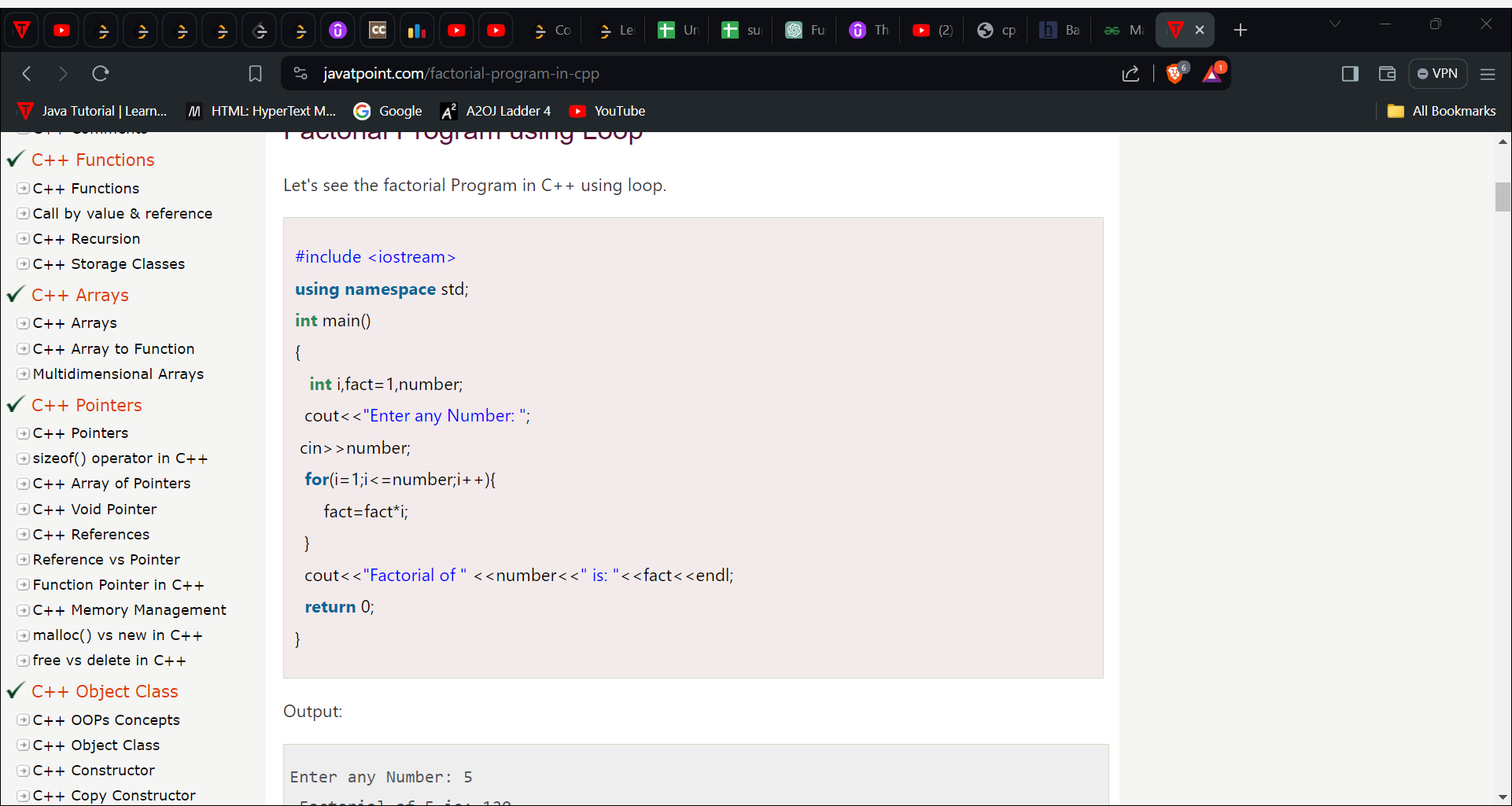
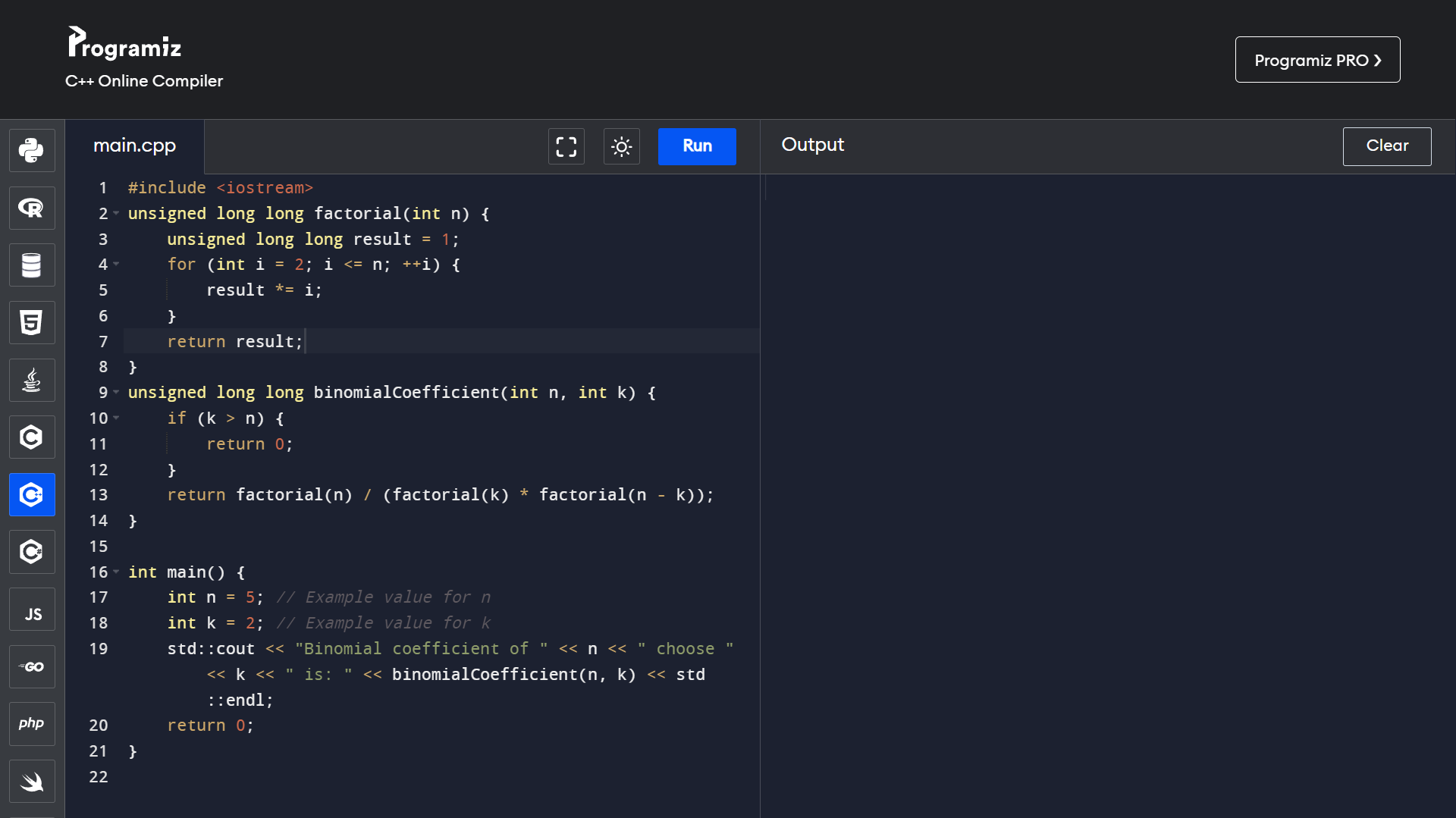
Factorial of a number n is defined as a product of all positive descending integers, Factorial of n is denoted by n!. Factorial can be calculated using the following recursive formula where the recursive call is made to a multiplicity of all the numbers lesser than the number for which the factorial is computed as the formula to calculate factorial is as follows:

n! = n * [(n-1)!]

i.e factorial of n - (n!) = n * (n-1) * ……* 3 * 2* 1.

Note: Factorial of 0 is 1.

Factorial Program using Loop:

Factorial Program in C++ - javatpoint - Brave

Factorial Program using Recursion:

Permutation

Permutation is defined as a mathematical calculation that tells us the way a particular set of data are arranged in a particular way. In simple word we can say that permutation is the number of ways objects can be ordered and arranged.

If n objects are available and we arrange all, then every arrangement possible is called a permutation. In other words, arranging some objects in a specific order is called permutation. For example, we need to choose two numbers out of {1, 2, 3}, then there can be 6 ways in which we can do the same. (1, 2), (2, 1), (2, 3), (3, 2), (1, 3), and (3, 1). As we can see here both (1, 2) and (2, 1) are two different permutations, unlike combinations where (1, 2) and (2, 1) are the same combination.

Representation of Permutation:

P(n, r)

nPr
Pn,k

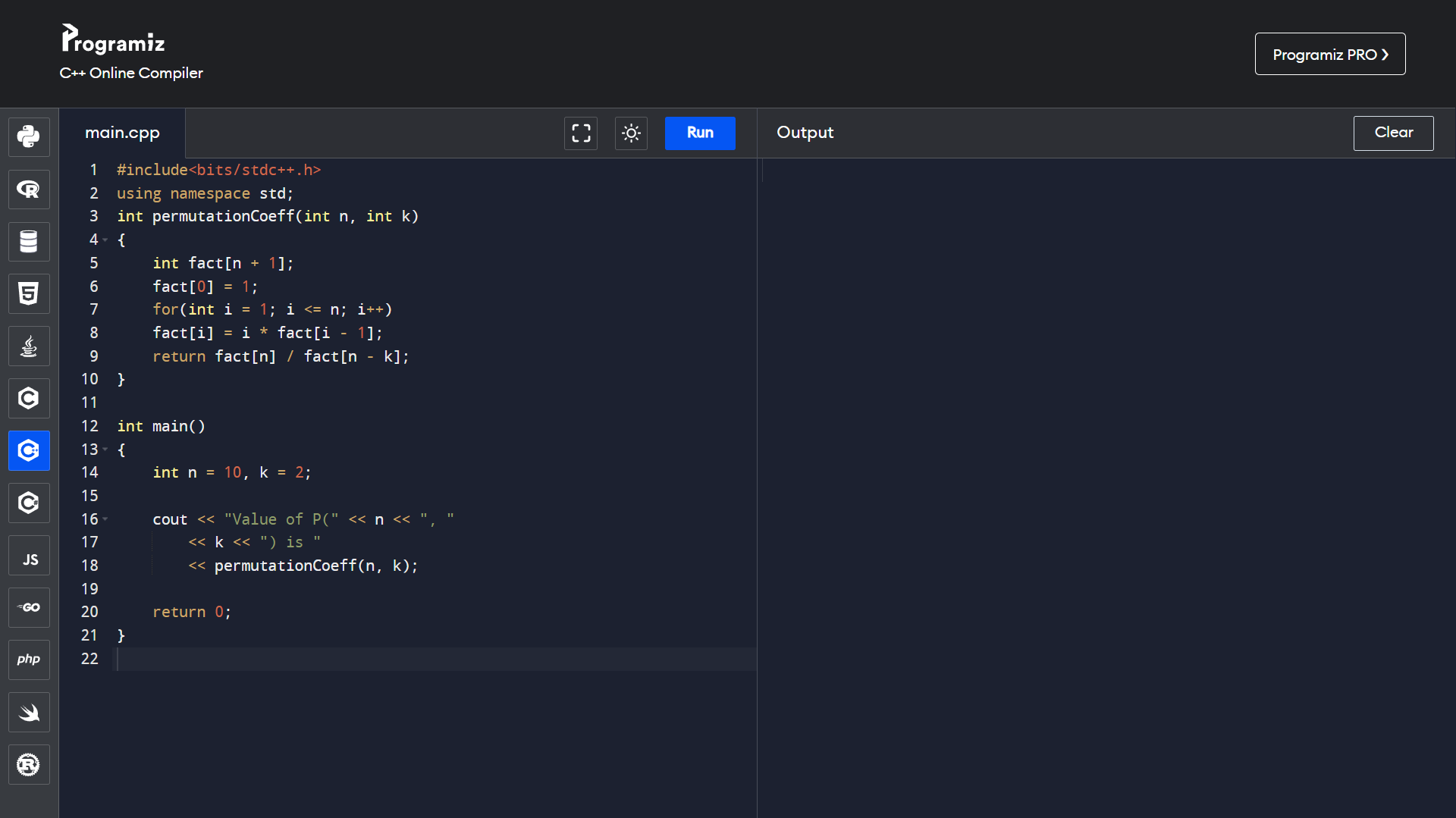
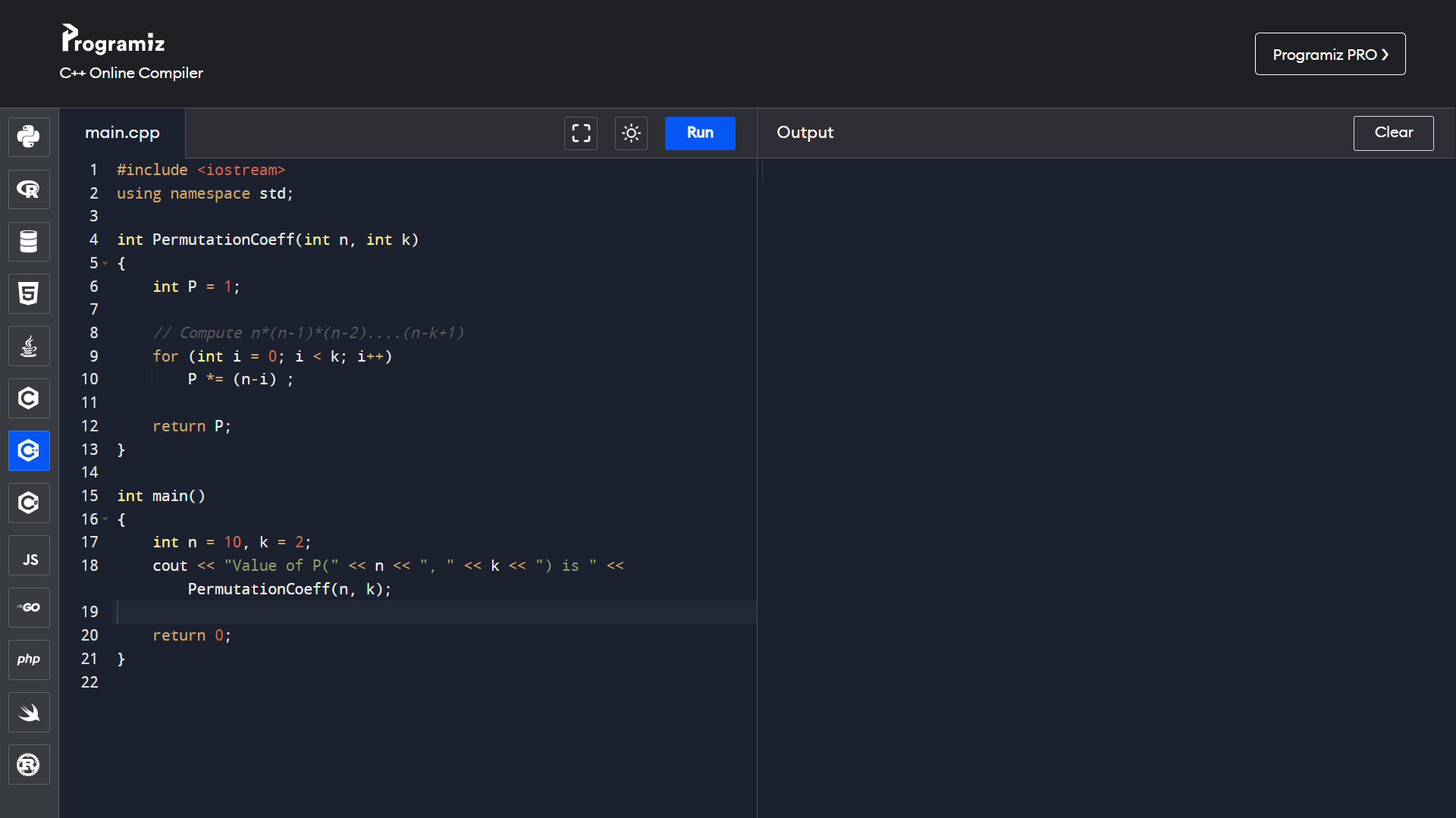
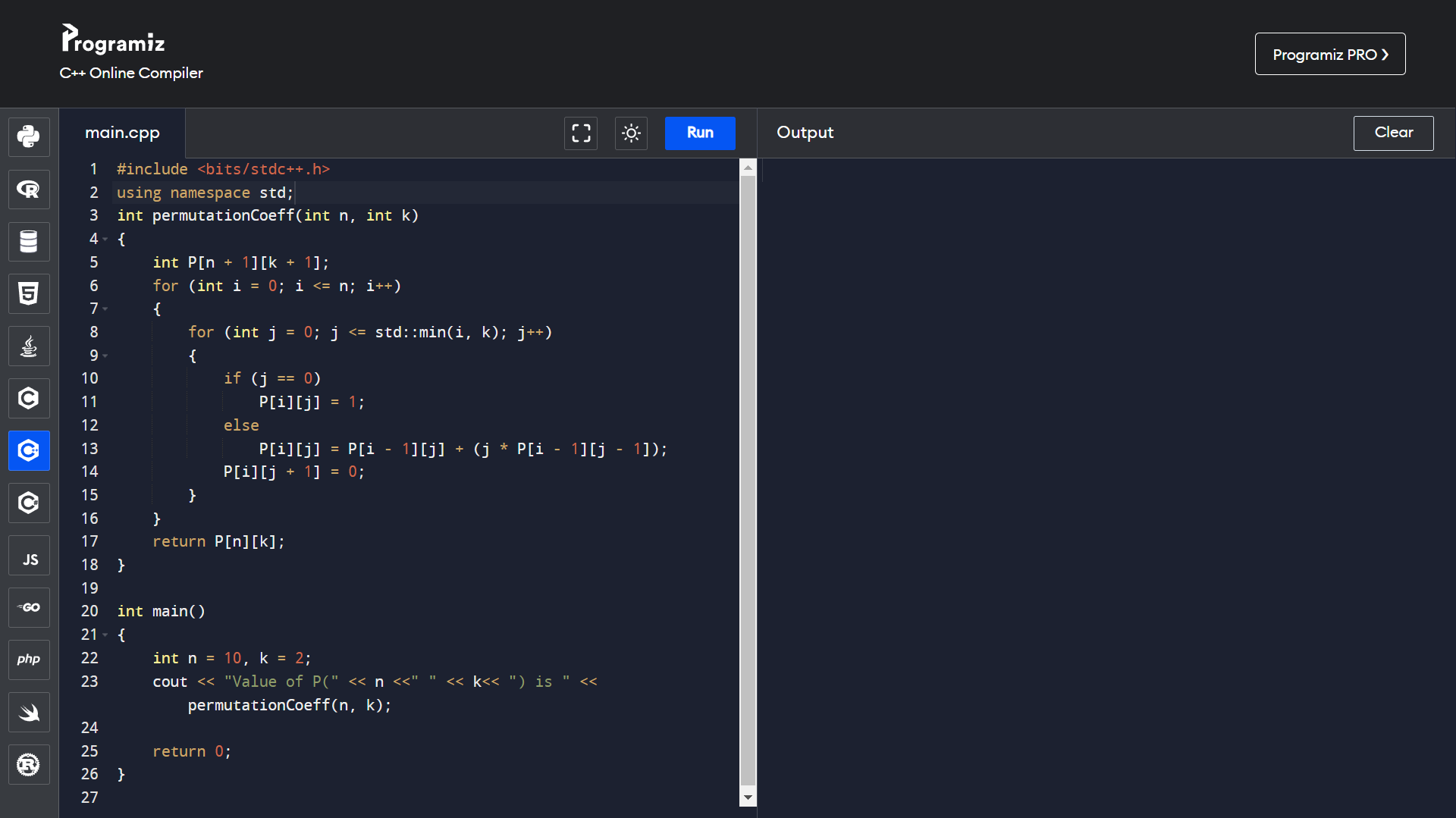
Permutation Formula ( nPr ):

P(n, r) = n! / (n-r)!

where,

n is the Number of Total Objects

**r **is the Number of Objects Chosen at Once

0 ≤ r ≤ n

Types of Permutation:

In the study of permutation, there are some cases such as:

Permutation with Repetition

Permutation without Repetition

Permutation of Multi-Sets

Permutation With Repetition:

This is the simplest of the lot. In such problems, the objects can be repeated. Let’s understand these problems with some examples.

Example: How many 3-digit numbers greater than 500 can be formed using 3, 4, 5, and 7?

Since a three-digit number, greater than 500 will have either 5 or 7 at its hundredth place, we have 2 choices for this place.

There is no restriction on repetition of the digits, hence for the remaining 2 digits we have 4 choices each

So the total permutations are,

2 × 4 × 4 = 32

Permutation Without Repetition:

In this class of problems, the repetition of objects is not allowed. Let’s understand these problems with some examples.

Example: How many 3-digit numbers divisible by 3 can be formed using digits 2, 4, 6, and 8 without repetition?

For a number to be divisible by 3, the sum of it digits must be divisible by 3.

From the given set, various arrangements like 444 can be formed but since repetition isn’t allowed we won’t be considering them.

We are left with just 2 cases i.e. 2, 4, 6 and 4, 6, 8

Number of arrangements are 3! in each case

Hence the total number of permutations are: 3! + 3! = 12

Permutation of Multi-Sets:

Permutation when the objects are not distinct

This can be thought of as the distribution of n objects into r boxes where the repetition of objects is allowed and any box can hold any number of objects.

1st box can hold n objects

2nd box can hold n objects

3rd box can hold n objects

. .

. .

. .

rth box can hold n objects

Hence total number of arrangements are,

n × n × n . . . (r times) = nr

Example: A police officer visits the crime scene 3 times a week for investigation. Find the number of ways to schedule his visit if there is no restriction on the number of visits per day?

Number of ways to schedule first visit is 7 (any of the 7 days)

Number of ways to schedule second visit is 7 (any of the 7 days)

Number of ways to schedule third visit is 7 (any of the 7 days)

Hence, the number of ways to schedule first and second and third visit is

7 × 7 × 7 = 7³ = 343.

Programs for permutations coefficient:

Using the factorial:

Just using the formula:

Using dynamic programming:

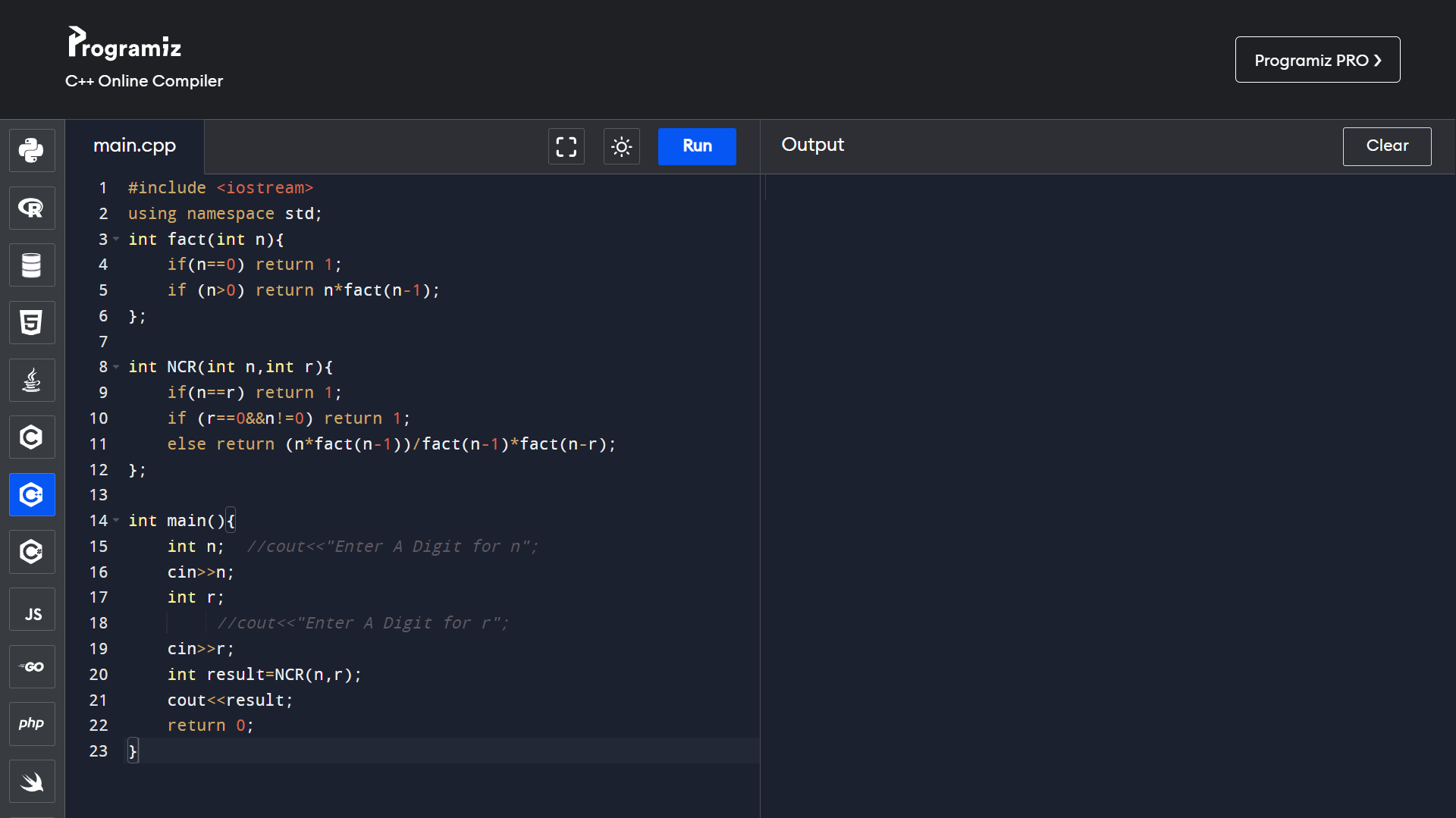
Online C++ Compiler - Brave

Combination

Combination is a way of choosing items from a set, such as (unlike permutations) the order of selection doesn’t matter. In smaller cases, it’s possible to count the number of combinations. Combination refers to the mixture of n things taken k at a time without repetition. To know the combinations in the case where repetition is allowed, the terms like k-selection or k-combination along with repetition are often used. For instance, if we’ve two elements A and B, then there’s just one way to select two items, we select both of them.

Combination is the choice of selecting r things from a group of n things without replacement and where the order of selection is not important.

Number of combinations when ‘r’ elements are selected out of a complete set of ‘n’ elements is denoted by nCr.

Representation of Combination:

C(n, r)

nCr
Cn,k

Combination Formula ( nCr ):

C(n, r) = n! / ((n-r)! * r!)

where,

n is the Number of Total Objects

**r **is the Number of Objects Chosen at Once

0 ≤ r ≤ n

Example:

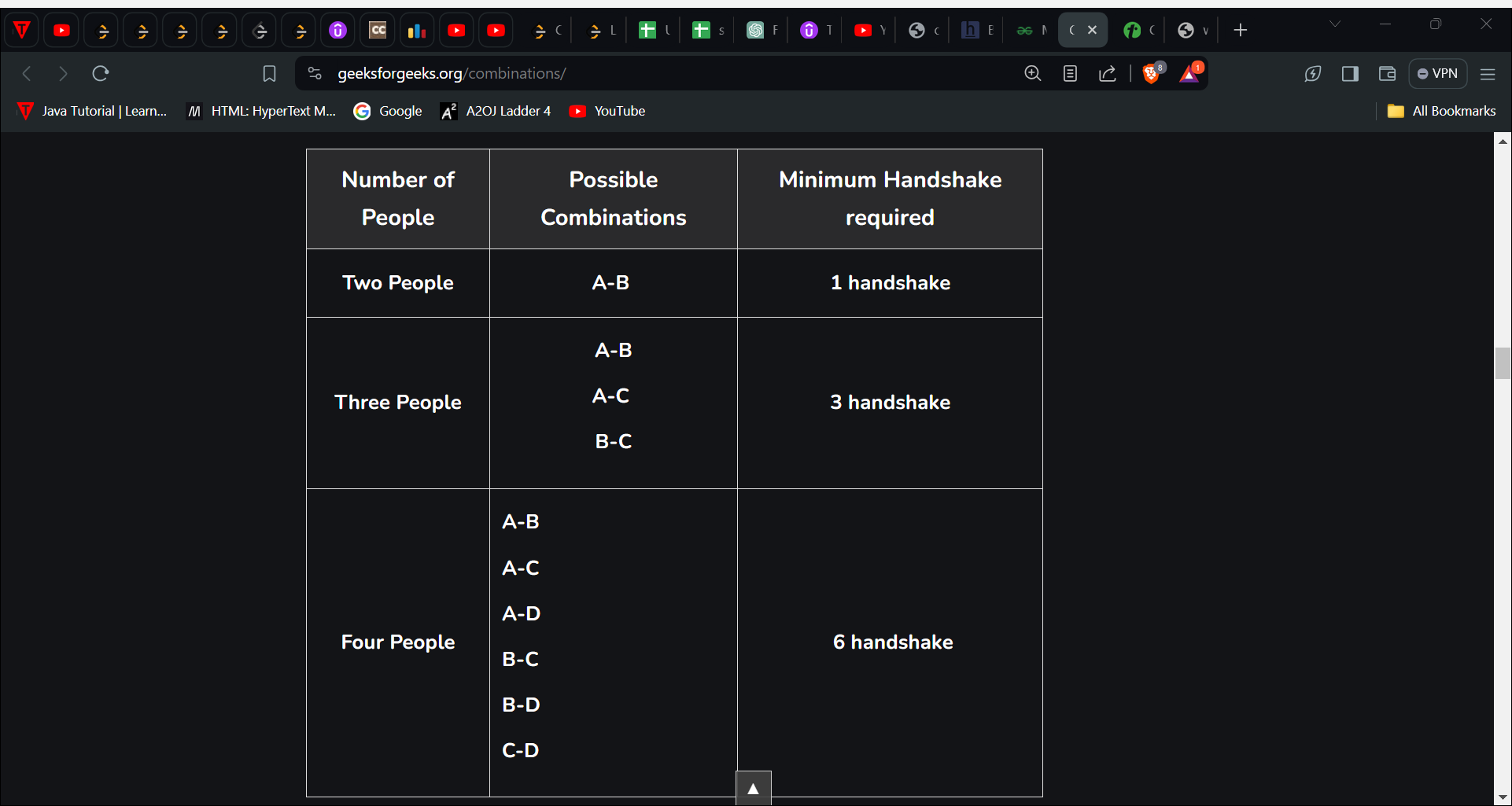
Handshaking problem:

Handshaking problem is one of the most interesting problems in combination. It is used to find that in a room full of people how many handshakes are required for everybody to shake everybody else’s hand exactly once.

Basically when there are 2 people there will be one handshake and if there are three people there will be 3 handshakes and so on. This many people we can count but let’s suppose there are thousands of people in a hall then we can’t count each handshake here the need for the combination arises.

Combinations - Definition, Formula, Solved Examples, FAQs - Brave

To see the people present, and consider one person at a time. The first person will shake hands with n – 1 other people. The next person will shake hands with n-2 other people, not counting the first person again. Following this, it will give us a total number of

(n – 1) + (n – 2) + … + 2 + 1

= n(n – 1)/ 2 handshakes.

Total Number of Handshakes = n × (n – 1)/2

Total Number of Handshakes = nC2

Properties of combination coefficient:

ⁿCr = ⁿCn-r.
ⁿCx = ⁿCy, then either x = y or x + y = n.
Recursive formula for combination:

ⁿ^-1Cr + ^n-1Cr_-1 = ⁿCr

ⁿCr + ⁿCr₊₁ = ⁿ⁺¹Cr₊₁

Programs for combination coefficient:

Using factorial function:

Using formula directly:

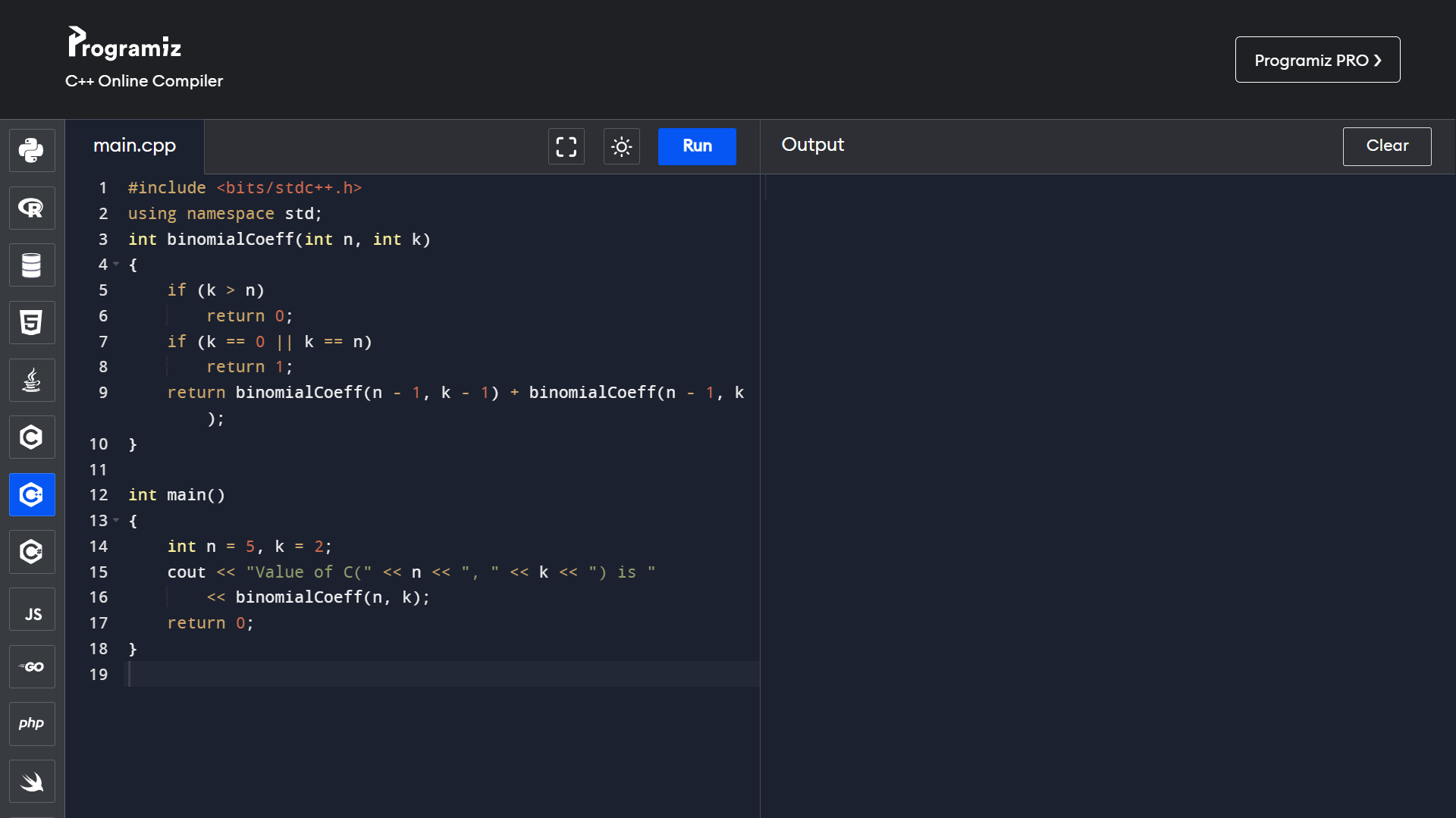
Binomial coefficient

A binomial coefficient C(n, k) can be defined as the coefficient of x^k in the expansion of (1 + x)^n.

A binomial coefficient C(n, k) also gives the number of ways, disregarding order, that k objects can be chosen from among n objects more formally, the number of k-element subsets (or k-combinations) of a n-element set.

(1+x)² = 1 + 2x + x² = ²C₀ + ²C₁ x+ ²C₂ x²

(1+x)³ = 1 + 3x + 3x² + x³ = ³C₀ + ³C₁ x+ ³C₂ x² + ³C₃ x³

So on.

Thus, we can see that combinations are only the binomial coefficients.

Example:

Consider expanding (x+2)⁵ :

(x+2)⁵=(x+2)(x+2)(x+2)(x+2)(x+2)

One quickly realizes that this is a very tedious calculation involving multiple applications of the distributive property. The binomial theorem provides a method of expanding binomials raised to powers without directly multiplying each factor:

(x+y)ⁿ = ⁿC₀ xⁿ y⁰ + ⁿC₁ x^n-1 y¹ + ⁿC₂ x^n-2 y² +….. .. . . . .+ ⁿC_n-1 x¹ y^n-1 + ⁿC_n x⁰ yⁿ

More compactly we can write,

(x+y)ⁿ= $\sum_{k = 0}^{n}{}$ ⁿC_k x^n-k y^k

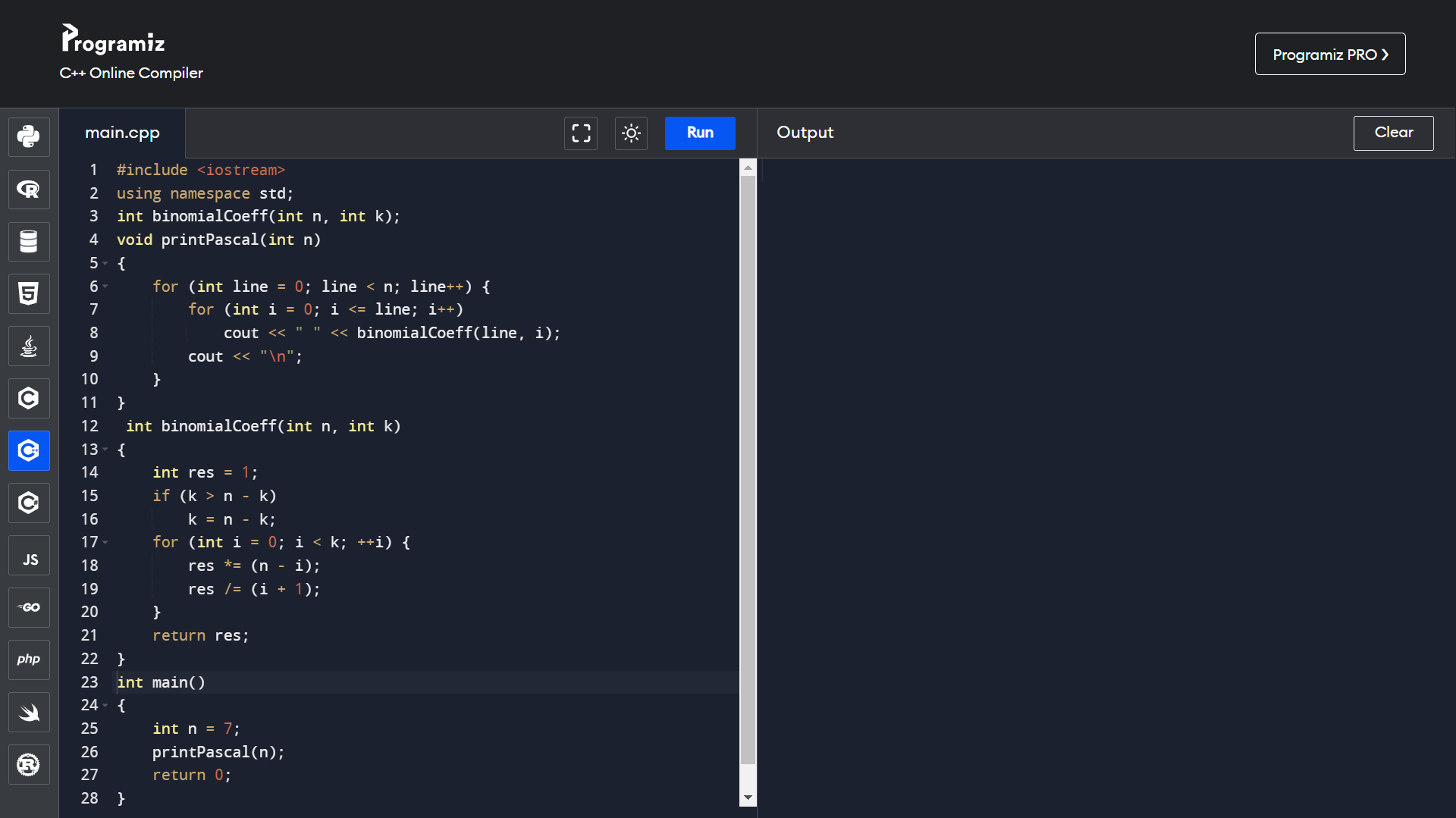
Program to find binomial coefficient:

Recursively:

The formula for recursively solving binomial coefficients.

C(n, k) = C(n-1, k-1) + C(n-1, k)

C(n, 0) = C(n, n) = 1

Online C++ Compiler - Brave

Using factorial by direct formula:

ⁿCr = n! / ( (n-r)! * r!)

Online C++ Compiler - Brave

Pascal’s Triangle

enter image description here

The image above is pascal’s triangle.

This is nothing but the coefficients of the terms of binomial expansion for different powers.

Pascal’s triangle is a never-ending equilateral triangle of numbers that follow a rule of adding the two numbers above to get the number below. Two of the sides are “all 1’s” and because the triangle is infinite, there is no “bottom side.”

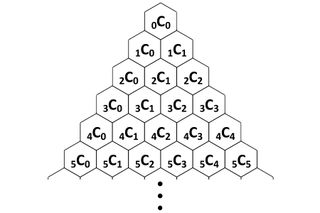
The numbers of Pascal’s triangle match the number of possible combinations (nCr) when faced with having to choose r-number of objects among n-number of available options.

Approach for program for pascal’s triangle:

The number of entries in every line is equal to line number. For example, the first line has “1“, the second line has “1 1“, the third line has “1 2 1“,.. and so on. Every entry in a line is value of a Binomial Coefficient. The value of ith entry in line number line is C(line, i). The value can be calculated using following formula.

C(line, i) = line! / ( (line-i)! * i! )

Program for pascal’s triangle:

Online C++ Compiler - Brave

Problems to practice for combinatorics:

PREVIOUSModular Arithmetic

NEXTPrefix and Suffix Sum